A continuación os proponemos una serie de ejercicios relacionados con cada una de las figuras geométricas presentadas anteriormente.
·Paralelepípedo
Ana quiere comprarse un escritorio para su ordenador. Como el ordenador tiene torre, quiere hacer una leja especial para ponerla. Sabiendo que la altura de la torre es de 40 cm y los lados del rectángulo base miden 20 y 10 cm respectivamente, calcula el espacio mínimo que debe dejar para la torre.
Solución: 8000 cm³
V = Ab · h
V = (10·20) · 40
V= 8000cm³
·Ortoedro
Pepito quiere introducir libros de 500cm³ de volumen en una caja cuyas dimensiones son las siguientes:
Lado a del rectángulo base: 37 cm
Lado b del rectánculo : 27 cm
Altura: 30 cm
¿Cuántos libros podrá introducir en la caja?
Solución: 54 libros
V = a · b · h
V = 37 · 27 · 30
V = 29970cm³
29970: 500 = 54
·Prismas
Hay que realizar una entrega de palillos Don Palillo. La entrega sería de 500 ejemplares. Sabiendo que la altura del prisma es 6 cm y el triángulo base es equilátero, midiendo 3 cm cada lado y su altura es de 2 cm, ¿qué espacio ocuparía la caja que los contuviera?
Solución= 9000cm³
V = Ab · h
V = 3 · 6
V = 18 cm³
18 · 500 = 9000cm³
V = 9000cm³
·Pirámides
Edelmira tiene una caja con forma de pirámide y quiere rellenarla con pirámides más pequeñas. Sabiendo que el volumen de la caja es de 6240cm³,y las pirámides más pequeñas cumplen las siguientes condiciones:
-Su AB es de 52cm².
-Su altura es de 15cm.
-Son amarillas.
Solución = 24 pirámides.
V = (AB · h ) : 3
V = (52 · 15 ) : 3
V = 780 : 3
V = 260 cm³
6240 : 260 = 24 pirámides.
·Cilindros
Lili quiere forrar unas latas de Fanta con papel de adorno dejando al descubierto la base superior para poder beber. Sabiendo que su AB es de 19.6 cm², su radio es de 2.5 cm, su generatriz de 12 cm y la altura de la lata es también de 12 cm, ¿cuántos cm2 de papel necesitaríamos para forrar 8 latas?
Solución = 29556.8 cm² de papel.
AT = AL · AB (Una única base ya que la superior la dejamos sin forrar)
AT = (2 · π · r · g) · 19.6
AT = 188.5 · 19.6
AT = 3694.6 cm²
3694.6 · 8 = 29556.8 cm²
·Conos
Una heladería ha encargado 48 cucuruchos de helado. Sabiendo que su radio es de 2 cm y su altura de 12cm, ¿qué cantidad de helado cabe dentro todos los cucuruchos?
Solución = 2412.48 cm³ de helado.
V = (π:3) · r2 · h
V = 50.26cm³
50.26·48 = 2412.48 cm³
·El cono truncado
Calcula el área lateral de un tronco de cono con las siguientes características:
-Su radio mayor es de 18 cm.
-Su radio menor es de 9 cm.
-Su generatriz es 20 cm.
Solución = 1696.5cm²
AL = π · (R + r) · g
AL = π · 27 · 20
AL = 1696.5cm²
·La pirámide truncada.
Calcula el volumen de una pirámide truncada sabiendo que:
-VB es 78cm³
-Vb es 47cm³
Solución = 31cm³
V = VB -Vb
V= 78 - 47
V = 31cm³
·Esfera.
Fran Fernández quiere hacer una bola del mundo para regalársela a su amigo José por su santo. José tiene una estántería con un hueco cuadrangular, en el cual cada cara mide 24.5 cm. ¿Qué dimensiones debería tener la bola del mundo que debe hacer Fran Fernández para que coja en la estantería de de José?
Solución = 4331.4 cm³
Hueco cuadrangular = 600.25 cm³
Radio esfera = 12.25cm
V = 3/4 · π · r³
V = 3/4 · 3.1416 · 1838.3
V = 4331.4 cm³
·Casquete esférico
Calcula el área de un casquete esférico sabiendo que:
-Su radio es de 48cm.
-Su altura mide 89cm.
Solución = 26828.16 cm²
A = 2 · π · r · h
A = 6.28 · 48 · 89
A = 26828.16 cm²
·Cubo
Floren ha encargado unos altavoces con forma de cubo para su escritorio. Debe de decir cuanto quiere que midan y ella ha dicho que quiere que mida de alto 6 cm. ¿Cuál será el volumen de sus nuevos altavoces?
Solución = 216 cm³
V = a³
V = 6³
V = 216 cm³
·Tetraedro
Antonia quiere encargar calendarios con forma de tetraedro. Para su transporte tiene una caja de 4561cm³ de volumen. Sabiendo que la base es un triángulo equilátero de 8 cm de lado y los lados de los triángulos que forman sus caras son isósceles, de 15 cm de lado.
Solución = 397.75cm³
V = a³/12 · raíz cuadrada de 2
V = 281.25 · 1.4142
V = 397.75cm³
·Octaedro
Cucum quiere hacerse una peonza de madera con forma de octaedro de 7 cm de arista para guardarla en una caja azul que le regaló su abuelo con un volumen 144cm³. ¿Podrá guardarla en la caja?
Solución = No, no podrá.
V = 1/3 · raíz cuadrada de 2 · a³
V = 0.47 · 7³
V = 161.21cm³
·Dodecaedro
Chari quiere forrar un dado. Dicho dado tiene 12 caras, las cuales miden 16cm, ¿qué cantidad de material necesitará?
Solución = 4577.04 cm²
AT = 15 · a² · √ (5 · 2 · √5) : 5
AT = 15 · 144 · √ 22.23 : 5
AT = 2160 · √ 4.446
AT = 2160 · 2.119
AT = 4577.04 cm²
·Icosaedro
Mónica Carlota se va a comprar un dado de 20 caras, para así ganar siempre al parchís. El dado es azul, pero a ella le gusta mas rosa, por lo que decide forrarlo. Los lados de dicho dado miden 3.5 cm. Calcula la cantidad de papel rosa que debe utilizar.
Solución = 105.35cm²
AT = 5 · a² · √3
AT = 5 · 12.25 · 1.72
AT = 105.35cm²
Y aquí acaban los ejercicios propuestos (soluciones incluidas) que os presentamos para mejorar vuestra geometría. Esperamos que os sirvan de ayuda.
Estructuras enlazadas que forman nuestro mundo.
En esta página os ofrecemos la información sobre los cuerpos geométricos que todos deberíamos saber.
lunes, 11 de junio de 2012
Teorema de Euler.
Este teorema recibe su nombre por su creador Leonhard Paul Euler.
Las consecuencias del teorema de Euler se pueden resumir en tres puntos:
1· No puede existir un poliedro convexo con menos de seis aristas, cuatro caras y cuatro vértices.
2· Sólo existen cinco poliedros convexos cuyas caras sean polígonos de igual número de lados y cuyos ángulos poliedros tengan entre si el mismo número de aristas y que son; tetraedro, octaedro, icosaedro, hexaedro y dodecaedro.
Las consecuencias del teorema de Euler se pueden resumir en tres puntos:
1· No puede existir un poliedro convexo con menos de seis aristas, cuatro caras y cuatro vértices.
2· Sólo existen cinco poliedros convexos cuyas caras sean polígonos de igual número de lados y cuyos ángulos poliedros tengan entre si el mismo número de aristas y que son; tetraedro, octaedro, icosaedro, hexaedro y dodecaedro.
3· La suma de todas las caras de un poliedro convexo es igual a tantas veces cuatro rectos como el número de vértices que tiene menos dos.
Este teorema tiene un principio que dice: en todo poliedro convexo, el número de caras más el de vértices, es igual al de aristas más dos.
Ese principio se representaría con la siguiente fórmula:
C + V = A + 2
Donde C es el número de caras, V el de vértices y A el de aristas.
Este teorema tiene un principio que dice: en todo poliedro convexo, el número de caras más el de vértices, es igual al de aristas más dos.
Ese principio se representaría con la siguiente fórmula:
Donde C es el número de caras, V el de vértices y A el de aristas.
Teorema de Cavilieri en el espacio.
Este teorema recibe este nombre por su creador, Bonaventura Cavilieri. Se podría decir que es una ley geométrica que representa la diferencia de volumen entre dos cuerpos. La ley dice así:
Si dos cuerpos tienen la misma altura y además tienen igual área en sus secciones planas realizadas a una misma altura, poseen entonces igual volumen.
Si dos cuerpos tienen la misma altura y además tienen igual área en sus secciones planas realizadas a una misma altura, poseen entonces igual volumen.
domingo, 10 de junio de 2012
El icosaedro.
El icosaedro es un poliedro cuyas caras son triángulos equiláteros. Está constituido por 20 caras, 12 vértices y 30 aristas
Para calcular su área, necesitaremos la siguiente fórmula:
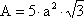
Mientras que para su volumen, esta fórmula:

El desarrollo plano de esta figura corresponde a este:

Que, una vez formado, da la siguiente figura:

La cual encontramos en diferentes objetos, como:

Y estos son los detalles básicos que debemos conocer a cerca del icosaedro.
Para calcular su área, necesitaremos la siguiente fórmula:
Mientras que para su volumen, esta fórmula:

El desarrollo plano de esta figura corresponde a este:
Que, una vez formado, da la siguiente figura:

La cual encontramos en diferentes objetos, como:
Y estos son los detalles básicos que debemos conocer a cerca del icosaedro.
El dodecaedro.
El dodecaedro es un poliedro de 12 caras con forma de pentágono. Este poliedro puede ser convexo o cóncavo. Está compuesto por sus doce caras, 20 vértices y 30 aristas.



La fórmula que usaremos para hallar su área total es la siguiente:
AT= 

El área de sus caras se calcularía con esta fórmula:
AL= 

Y, por último, si deseamos conocer su volumen, necesitaríamos utilizar la siguiente fórmula:
V= 

El desarrollo plano de esta figura sería como se representa en la siguiente imagen:
Al formar ese desarrollo plano, resultaría la siguiente figura:

Esta figura la podemos encontrar en objetos como este:

Y estos son los detalles básicos que todos debemos conocer a cerca de los dodecaedros.
El octaedro.
El octaedro es un cuerpo geométrico que consta de 8 caras, todas ellas formadas por triángulos equiláteros, 6 vértices y 12 aristas.
Para conocer su área total, la fórmula es la siguiente:

Y por último, para averiguar su volumen, necesitaremos la siguiente fórmula:
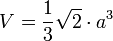
El desarrollo plano de esta figura corresponde a este:

Que, una vez formado, da la siguiente figura:

La podemos encontrar en diferentes objetos de nuestra vida, como:

Y estos son los detalles básicos que debemos conocer a cerca del octaedro.
Para conocer su área total, la fórmula es la siguiente:
Y por último, para averiguar su volumen, necesitaremos la siguiente fórmula:
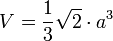
El desarrollo plano de esta figura corresponde a este:
Que, una vez formado, da la siguiente figura:

La podemos encontrar en diferentes objetos de nuestra vida, como:
Y estos son los detalles básicos que debemos conocer a cerca del octaedro.
El tetraedro.
El tetraedro es un poliedro de cuatro caras con forma de triángulos equiláteros. Esta formado por 4 caras (nombradas anteriormente), 6 vértices y 4 aristas.

.svg/220px-Tetrahedron_(PSF).svg.png)

Su área total se calcula con la siguiente fórmula:
AT = 

Donde a corresponde al apotema de la figura.
El área de una cara de esta figura se hallaría con esta fórmula:
AL = 

Finalmente, para calcular su volumen necesitamos conocer la siguiente fórmula:
V= 

El desarrollo plano del tetraedro sería así:
Una vez formada esta figura resultaría lo que veremos en la siguiente imagen:
.svg/220px-Tetrahedron_(PSF).svg.png)
Esta figura la podemos encontrar en objetos como el siguiente:
Y estos son los detalles básicos que todos debemos conocer a cerca de los tetraedros.
Suscribirse a:
Comentarios (Atom)